
< (4) 특성 스케일링 (Feature Scaling) >
# 전장에서 사용하였던 데이터프레임을 가지고와 이어서 진행
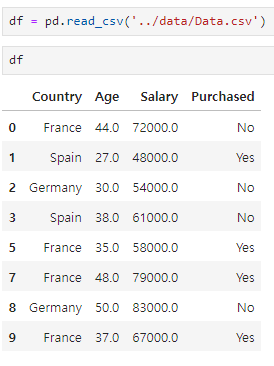
Age 와 Salary 는 같은 스케일이 아니다.
Age 는 27 ~ 50 Salary 는 40k ~ 90k (만단위)
# 유클리디언 디스턴스로 오차를 줄여 나가는데, 하나의 변수는 오차가 크고, 하나의 변수는 오차가 작으면, 나중에 오차를 수정할때 편중되게 된다.
# 따라서 값의 레인지를 맞춰줘야 정확히 트레이닝 된다.
< Feature Scaling 2가지 방법 >
- 표준화 : 평균을 기준으로 얼마나 떨어져 있느냐? 같은 기준으로 만드는 방법, 음수도 존재, 데이터의 최대최소값 모를때 사용.
- 정규화 : 0 ~ 1 사이로 맞추는 것. 데이터의 위치 비교가 가능, 데이터의 최대최소값 알떄 사용

# 이전에 학습한 표준화 혹은 정규화를 통해 데이터들의 범위를 맞춰줘야 한다.
# 피쳐 스케일링을 위한 스케일러는, X용과 y용 따로 만들어야 한다!! (중요!!) => 같이 쓸경우 오류가 발생될수 있음
# 임포트
from sklearn.preprocessing import StandardScaler, MinMaxScaler
# 이번 데이터는 두가지 모두 사용 가능하므로 두가지 모두 예제로 실행
# 1) 표준화
# X용 스텐다드 스케일러
X_scaler = StandardScaler()
X_scaler.fit_transform( X )
array([[ 1. , -0.57735027, -0.57735027, 0.69985807, 0.58989097],
[-1. , -0.57735027, 1.73205081, -1.51364653, -1.50749915],
[-1. , 1.73205081, -0.57735027, -1.12302807, -0.98315162],
[-1. , -0.57735027, 1.73205081, -0.08137885, -0.37141284],
[ 1. , -0.57735027, -0.57735027, -0.47199731, -0.6335866 ],
[ 1. , -0.57735027, -0.57735027, 1.22068269, 1.20162976],
[-1. , 1.73205081, -0.57735027, 1.48109499, 1.55119478],
[ 1. , -0.57735027, -0.57735027, -0.211585 , 0.1529347 ]])
# y는 이미 0과 1로만 구성되어 있어서 (가장 이상적) 해당 예제에서는 따로 스케일러 필요가 없다
y
array([0, 1, 0, 0, 1, 1, 0, 1])
# 2) 정규화 => 0과 1사이로 레인지
# X용 정규화 스케일러로 다시 설정하여 실행해보자
X_scaler = MinMaxScaler()
X = X_scaler.fit_transform( X )
X
array([[1. , 0. , 0. , 0.73913043, 0.68571429],
[0. , 0. , 1. , 0. , 0. ],
[0. , 1. , 0. , 0.13043478, 0.17142857],
[0. , 0. , 1. , 0.47826087, 0.37142857],
[1. , 0. , 0. , 0.34782609, 0.28571429],
[1. , 0. , 0. , 0.91304348, 0.88571429],
[0. , 1. , 0. , 1. , 1. ],
[1. , 0. , 0. , 0.43478261, 0.54285714]])ㄴ 정규화 데이터로 이후 진행
< Dataset을 Training 용과 Test용으로 나눈다 >
# 학습용 데이터를 테스트용으로 또 재사용해버리면 이미 학습한 데이터이기 때문에 의미가 없음
# 그러므로, 학습용과 시험용으로 분리해서 사용하여야 의미성이 있다.
# 머신러닝이 결국 이전 데이터로 학습하여 미래 데이터를 예측하는것이기 때문에 학습용을 테스트용으로 쓰면 의미가 없음
# 임포트
from sklearn.model_selection import train_test_split
# 순서는 절대 틀리면 안됨 train_test_split( 학습 변수 , 레이블링 변수 ,
# test_size= 어느정도를 테스트용을 쓸것인가?, random_state= 시드값과 같음 랜덤의 규칙을 정하는것 )
train_test_split( X , y, test_size=0.2, random_state=32 )
ㄴ 해당 예제문은 학습 변수 X , 레이블링 변수 y , 학습은 80% 테스트는 20%로 설정, 시드값은 32 로 짠것
[array([[1. , 0. , 0. , 0.73913043, 0.68571429],
[0. , 1. , 0. , 0.13043478, 0.17142857],
[1. , 0. , 0. , 0.34782609, 0.28571429],
[1. , 0. , 0. , 0.91304348, 0.88571429],
[0. , 0. , 1. , 0.47826087, 0.37142857],
[1. , 0. , 0. , 0.43478261, 0.54285714]]),
array([[0., 1., 0., 1., 1.],
[0., 0., 1., 0., 0.]]),
array([0, 0, 1, 1, 0, 1]),
array([0, 1])]
# train_test_split 함수를 사용하면 결과값이 4개로 출력됨
# 그러므로 각 네개 결과값을 연속으로 변수로 지정할수 있다.
# 변수 지정시에도 train, test 순서를 절대 바꾸지 말고 그대로 사용하여야함
X_train, X_test, y_train, y_test = train_test_split( X , y, test_size=0.2, random_state=32 )
# train 으로 트레이닝 값 확인
X_train
array([[1. , 0. , 0. , 0.73913043, 0.68571429],
[0. , 1. , 0. , 0.13043478, 0.17142857],
[1. , 0. , 0. , 0.34782609, 0.28571429],
[1. , 0. , 0. , 0.91304348, 0.88571429],
[0. , 0. , 1. , 0.47826087, 0.37142857],
[1. , 0. , 0. , 0.43478261, 0.54285714]])
y_train
array([0, 0, 1, 1, 0, 1])
# test로 테스트값 확인
X_test
array([[0., 1., 0., 1., 1.],
[0., 0., 1., 0., 0.]])
y_test
array([0, 1])